田渊栋大佬新作！o1都搞不定的旅行规划问题有办法了！传统符号推理和大模型推理的融合之路

本文由readlecture.cn转录总结。ReadLecture专注于音、视频转录、总结和翻译，2小时视频，5分钟阅读，加速内容学习与传播。

视频来源

bilibili: https://www.bilibili.com/video/BV1vGmRYgEod?p=1

大纲

总结

一句话总结

本文探讨了如何将神经推理与符号推理结合，以解决大模型在推理和规划问题上的不足，并介绍了相关研究和应用案例。

结论

大模型在推理和规划问题上仍存在不足，如GPT-4-Turbo在旅行规划问题上的通过率仅为0.6%。
通过结合符号推理系统，可以显著提高大模型在复杂规划问题上的表现。
使用混合整数规划求解器（MILP）可以在短时间内提供有保证的最优解。
通过Agent Constitution训练的Agent在处理复杂问题时表现优于传统大模型。
神经网络学出的解可能具有符号结构，这为神经网络与符号系统的结合提供了新的可能性。

深度问答

大模型在推理和规划问题上的主要挑战是什么？
- 主要挑战是模型生成的计划通过率低，存在遗漏条件和前后矛盾等问题。
如何通过结合符号推理系统来提高大模型的表现？
- 通过将用户的输入转化为符号表示，并使用求解器（如MILP）来获得最优解，然后将结果翻译成自然语言输出。
Agent Constitution的主要作用是什么？
- 规定Agent在每个步骤上的要求，确保最终答案准确、高效，并减少错误。
神经网络学出的解可能具有什么结构？
- 可能具有符号结构，这表明神经网络的解在深层层次上可以与符号系统统一。
如何通过代数结构来优化神经网络的训练？
- 通过构造满足某些子条件的部分解，并将这些解相乘和相加，最终得到全局最优解。

关键词标签

大模型
神经推理
符号推理
规划问题
混合系统

目标受众

人工智能研究人员
数据科学家
软件工程师
对AI技术感兴趣的学生
企业决策者

术语解释

大模型 (Large Model): 指具有大量参数和复杂结构的机器学习模型，如GPT-4。
符号推理 (Symbolic Reasoning): 使用符号和逻辑规则进行推理的方法。
混合整数规划 (Mixed Integer Linear Programming, MILP): 一种数学优化技术，用于求解包含整数变量的线性规划问题。
Agent Constitution: 规定Agent在每个步骤上的要求，确保其行为符合预期。
代数结构 (Algebraic Structure): 在数学中，指具有特定运算和性质的集合。

内容回顾

这次接到你们的邀请，来到AI TIME进行讲座。我现在在Meta AI的FAIR担任研究总监，管理一个团队，主要任务是研究大模型上的推理和规划等问题。这次我会讲解如何将神经推理与符号推理结合起来，形成一个更强大的系统。由于大家可能都是华人，中文交流更为方便，所以我将用中文进行讲解。

然后我们就开始吧。 大家都知道，大模型在最近是一个非常火热的方向。大家都看到有很多应用，包括用它来做对话、生成各种内容、用作agent等。当然，大模型一个比较核心的功能是用它来做推理和规划。

当然，在这个方向上，其实还有很多问题尚未解决，这也是我们选择这个方向的原因。这是一个非常简单的例子，可以说明当前大模型在这方面仍然不够成熟。

这个例子是关于旅行规划的。旅行规划问题是一个场景，比如，作为一个用户，我可能会向大模型发出指令，告诉他我要去夏威夷，待几天，预算为5000元，并希望某些航班，希望在某天到达，希望在那边待几天，希望与谁见面等要求。在提出这些要求后，将这些要求全部发送给大模型，原则上可以让大模型通过收集信息来处理。

然后，收集完信息后，让大模型进行规划（planning）。通过这种方式，大模型应该能提供一个非常具体的规划流程。例如，第一天去哪里，第二天去哪里，最后一天去哪里。原则上，你应该有一个非常详细的计划。

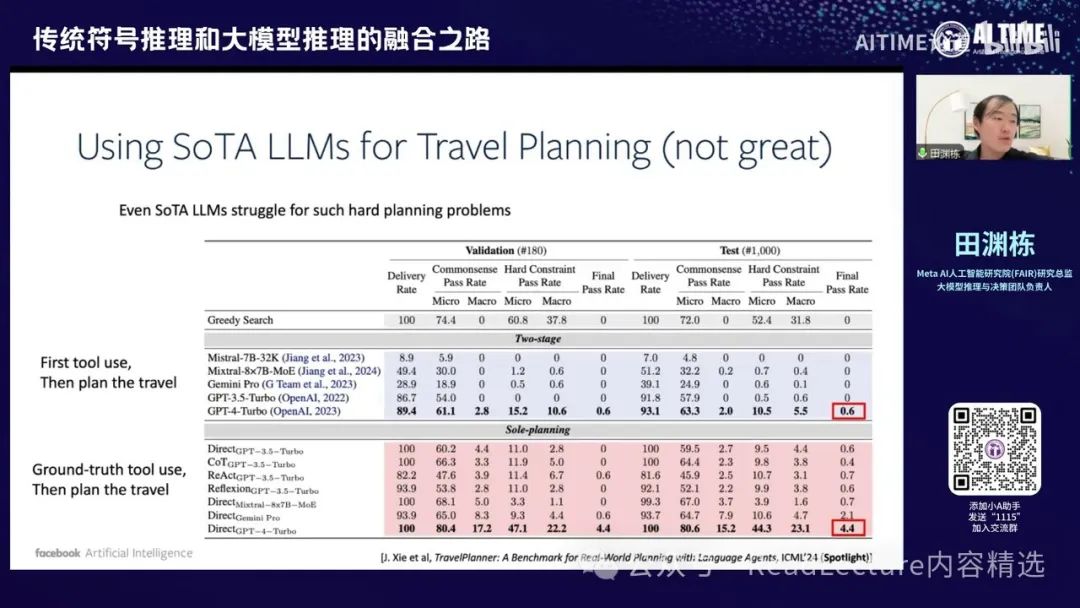
但是，如果你真的用大模型来做这样的规划问题，其实现在的效果并不理想。 这篇文章是我们今年ICML 2024的Spotlight文章，文章中提到，我们当时使用的最好的模型是GPT-4-Turbo。这个模型生成的旅行计划通过率只有0.6%，即6‰，这个数字非常小，意味着大部分计划无法通过任何检测。它存在很多问题，比如有时会遗漏一些条件或要求，或者最终的计划有前后矛盾的地方，这些都是错误。即使是很强的GPT-4模型也做不到这一点。当然，如果我们允许大模型只做规划，去掉前面的工具调用部分，那么通过率会提高到4.4%，但这个数字仍然不高。

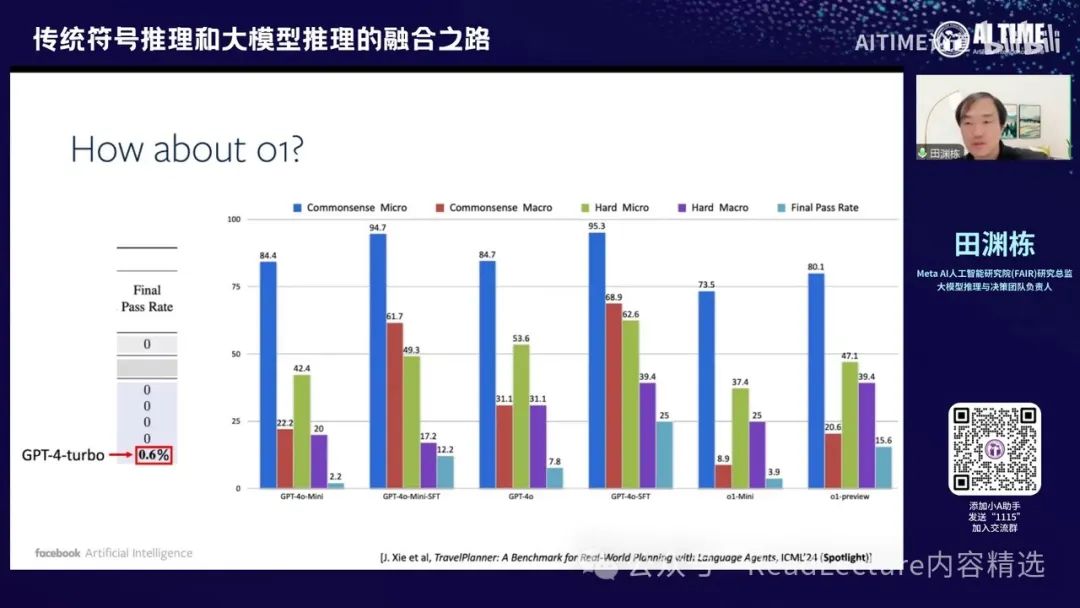
当然，大家可能会觉得，也许以前的GPT-4 Turbo表现不佳，我们是否可以换成O1呢？其实，我们最近也尝试了一下，发现效果并没有特别好。你会发现，在O1这个动作下，它的效果其实也没有达到之前的效果。所以，它的数字本身也是比较低的，虽然比原来高一点，但并没有达到特别好的程度。当然，这种方法其实还不如我用GPT-4在这些数据上微调一下，得到的效果更好，他会更好一点的25%，但就算这样，效果也没有特别好。所以，这些东西都是一个比较难的问题。

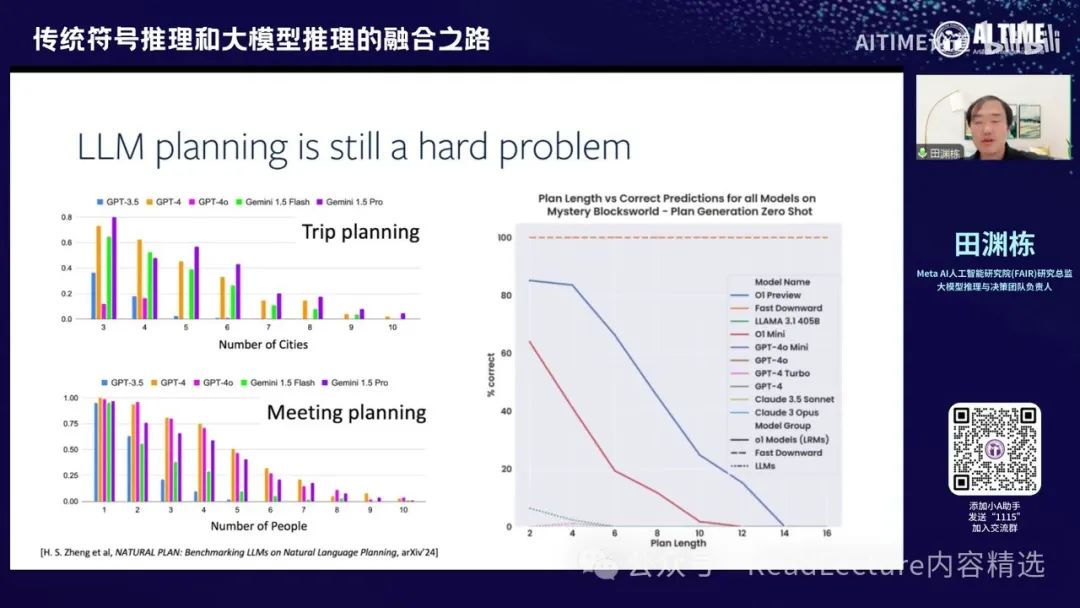
当然了，除了旅行规划之外，其实还有很多问题具有相似的特征。例如，GEMINI有一篇文章叫Natural Plan，这篇文章实际上是使用GEMINI来解决类似的规划问题，包括旅行规划和会议规划。你会发现，尽管GEMINI在某些情况下可能比GPT-4的效果还要好，但这种趋势是不可改变的。

这个趋势表明，横轴是问题的复杂度，例如对于旅行规划来说，涉及的城市越多，规划的正确性就越低，最终会变为零。对于会议规划也是如此，涉及的人数越多，成功的概率也会变为零。

最近的O1和O1 Mini，你会发现它们的效果其实也差不多，尽管一开始对较短的规划效果非常好，甚至远远超过之前的模型水平，但一旦问题变得更复杂，你会发现这两条线的下降速度其实也很快，很快就会与其他模型一样，大家都答不出来。

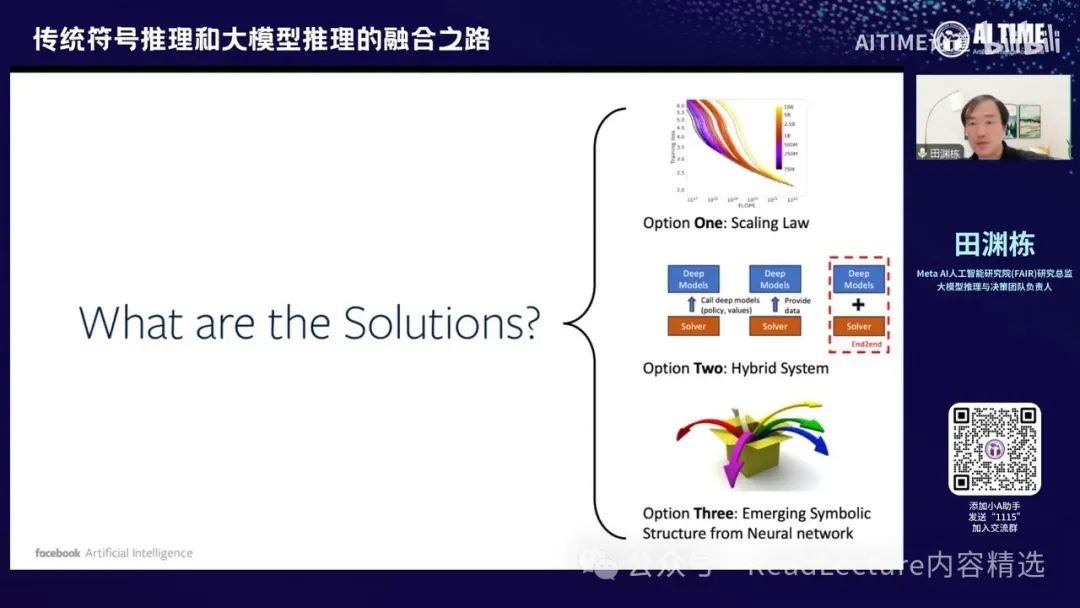
因此，对于规划问题，大模型目前仍难以取得非常理想的结果。当然，已有一些可能的解决方案，我将在接下来的讲解中进一步讨论。

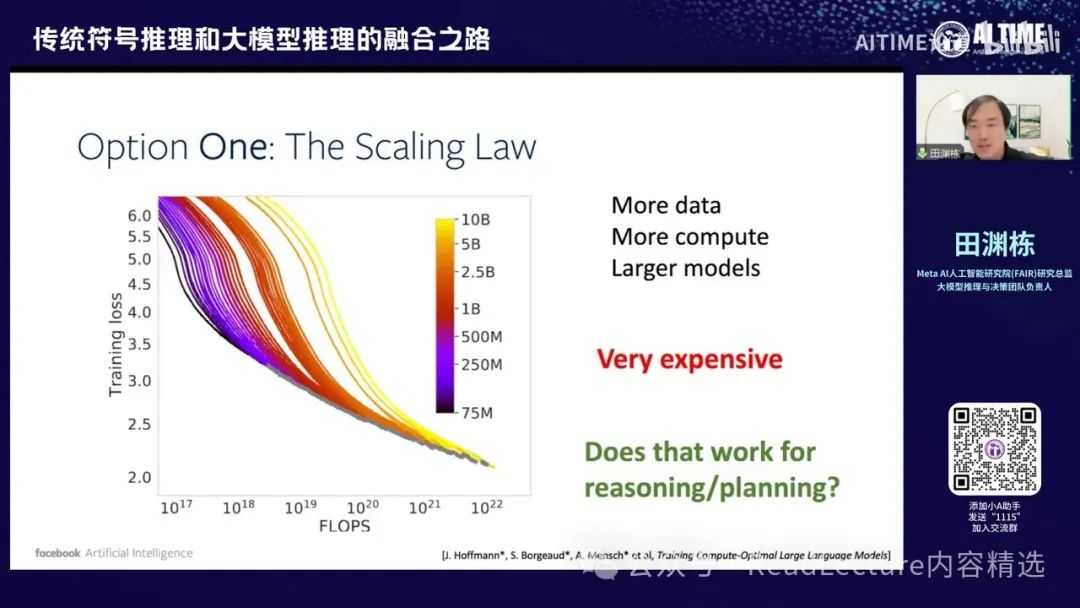
比如说，方案一当然是大家会想到的，就是Scaling Law，即增加数据、增加计算量，让模型变得更大。通过这种方式，也许有一天我们能够解决这些规划问题。当然，这种方法非常昂贵，需要花费大量金钱、精力和资源。最近，大家可能也在逐渐反思，是否Scaling Law这条路并没有那么容易走，这也是一个较大的问题。

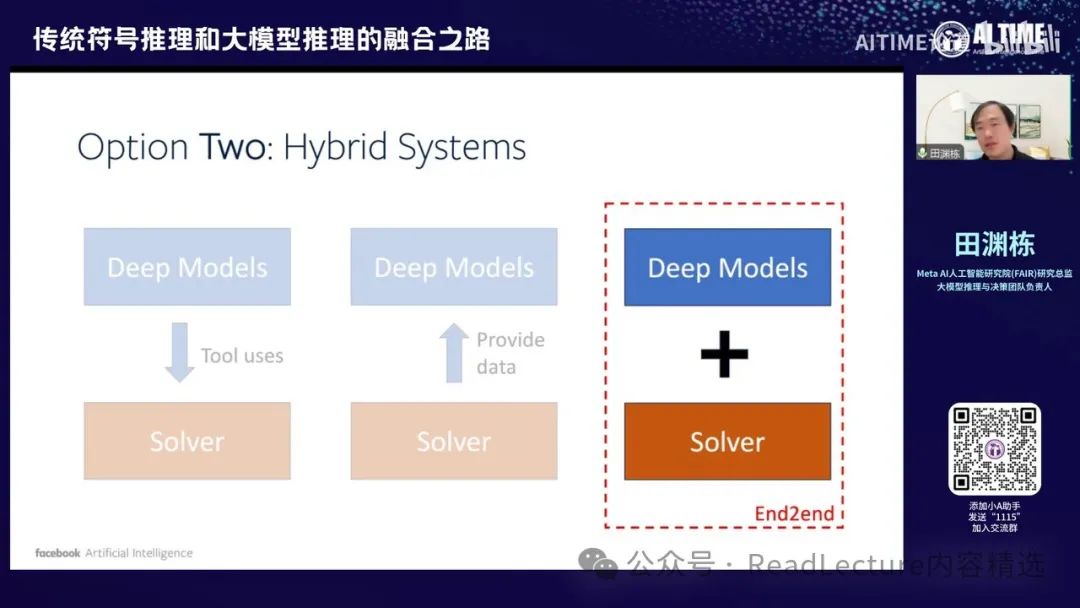
那么第二个方向是通过构建一个混合系统。我们知道大模型在自然语言理解方面表现出色，但同时也存在一些符号推理系统，这些系统非常擅长解决特定问题，并且其结果具有理论保证。这些求解器在大模型之前就已经存在。通过这些求解器，我们可以获得更好的结果。如果这两者能够互补，我们就可以构建一个系统，既能处理人类的自然语言输入，又能解决复杂的规划问题。这就是Option Two。

最后，Option Three是最近发现的一个有趣现象，即神经网络学出的解本身可能具有符号结构。这可能意味着我们可以在较深的层次中找到神经网络的符号结构与神经网络解之间的关系。这两者可能在非常深的层次上是可以统一的，而不需要像Option Two那样构建两个系统并通过某种方式拼接。这是一个较远的趋势，但目前已有一些文章显示出这种可能性。

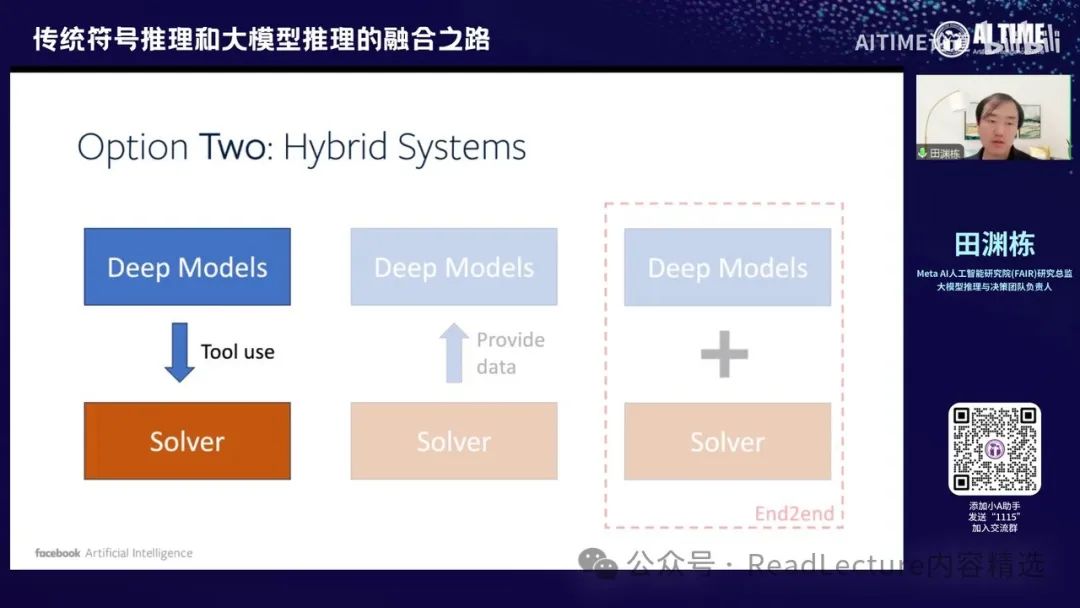
这种趋势下，我们现在开始讨论一些选择。具体来说，我们可以介绍一个工作，即我们仍然使用大模型，但同时将求解器纳入求解过程中。通过求解器，我们可以获得更优的输出解。

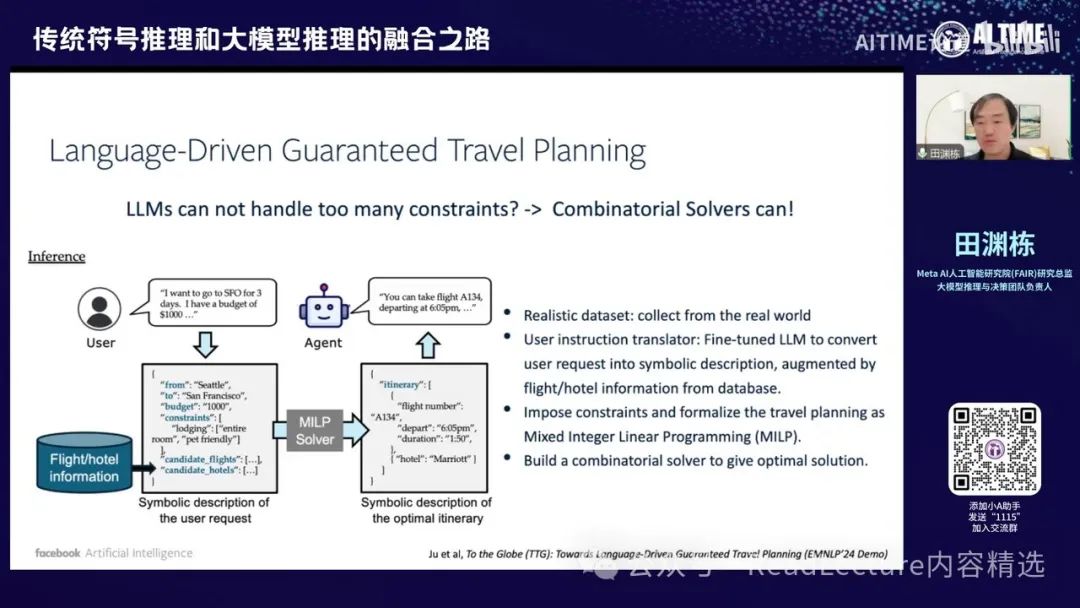
那么这一块呢，其实我们最近有一些工作，比如我们最近有一篇EMNLP24的Demo论文。这篇论文主要是关于旅行规划（Travel Planning）问题，这个问题其实非常难。 现在一方面我们可以用大模型来解决，另一方面，我们是否可以先将用户的输入转化为一个关于这次旅行的符号表示（symbolic description）。这个符号表示结合当时的机场和酒店信息，我们可以调用一个求解器，即混合整数规划（Mixed Integer Linear Programming， MILP）求解器。 这个求解器能够在短时间内给出一个最优解，并且这个最优解是有保证的，它一定是最优的，并且满足所有条件。然后，我们可以将这个最优解再翻译成自然语言的输出。这样，通过这种方式，我们给定一个自然语言输入，就可以得到一个非常准确的路径描述，从而解决旅行规划问题。

那么这部分内容，文章中已经制作了一个演示。这个演示几乎是实时的，你可以在大约2.5秒内将输入翻译成一个JSON格式的符号表示，然后在半秒内解出结果，并返回最终的规划结果。我们进行了一些人类实验，用户反馈表明他们对这个系统比较满意。之后，我们还可以进一步改进。

例如，对于之前的版本，旅行规划问题的表述是将所有信息用一句话连接起来，这种方式其实不太符合人类的表达习惯。 通常人们不会将所有旅行规划用一句话表达出来，而是通过对话逐步明确需求。因此，我们需要设计一个能够与用户交互的代理，通过交互过程逐步了解用户需求，并将其转化为JSON格式的符号表示。然后，可以使用求解器来处理这些符号表示。为了实现这一目标，

其实我们提出了一个名为Agent Constitution的概念，这个概念的目的是规定Agent在每个步骤上的要求。例如，我们希望Agent的最终答案必须是准确的，并且能够积极地提问。对于未搞清楚的问题，不能被动地回答，而是要主动询问。

我们还希望Agent能够高效地运作，以最短的方式，比如在十轮回答内收集到所有重要信息。最后，我们希望Agent在整个过程中尽量减少错误，避免产生幻觉或前后不一致的情况。

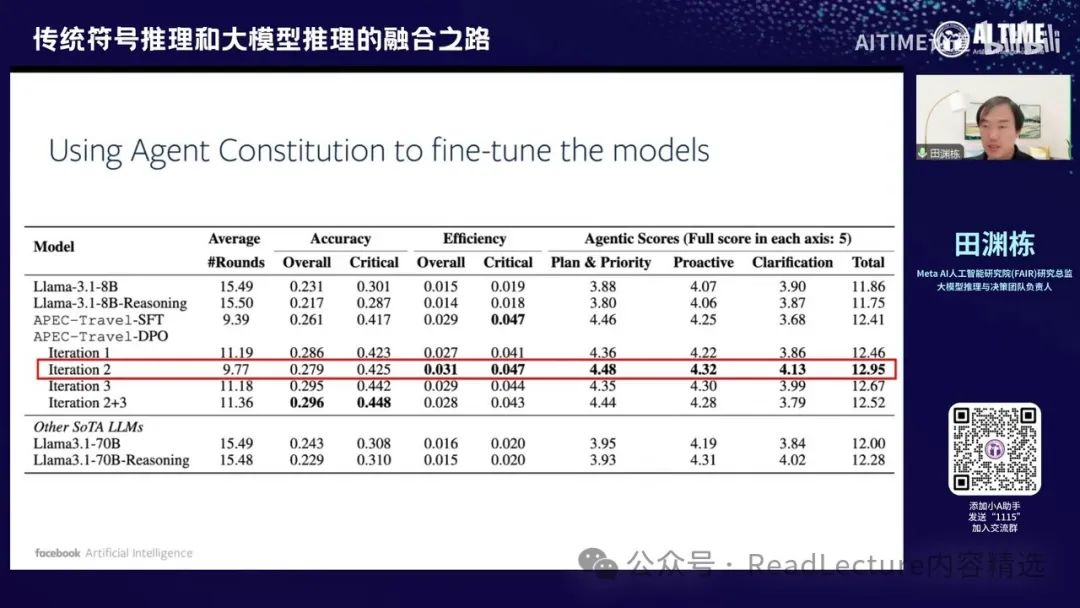
通过这种方式，我们可以利用 Agent Constitution 来训练 Agent。经过几轮训练后，Agent 的 Agentic Scores 都在逐步提升。确实，在经过两轮训练后，这些数字远远高于之前的 baseline。我们使用的模型是 8B 的简单模型，但其效果能够超过 70B 模型的效果。在经过翻停之后，效果显著。

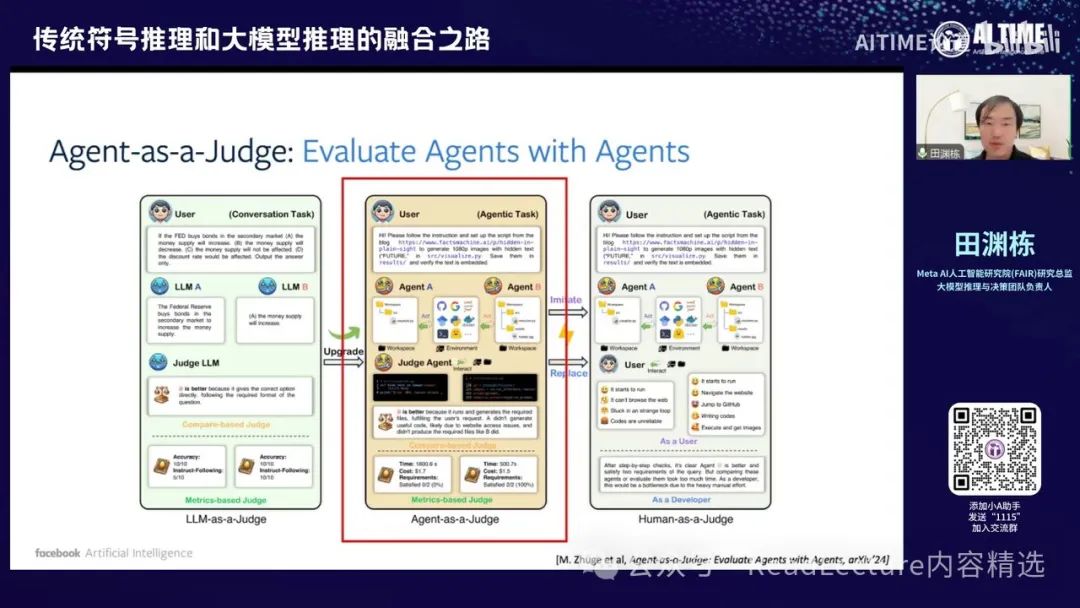
最近我们有一项工作，即使用Agent来担任整个评估过程的裁判。通常在评估一个问题时，需要花费大量时间和代价来判断问题的结构和答案是否正确。过去有些文章，如Agent-as-a-Judge，让大模型进行判断，看其结果是否正确。然而，另一方面，如果使用人类来做裁判，人类可能会更细致地观察每一步的走法，从而给出更详细、准确的反馈。

这篇文章提出，由于人类反馈较慢且成本高，可以使用Agent来模拟人类的反馈，这种反馈既快速高效，效果也很好。

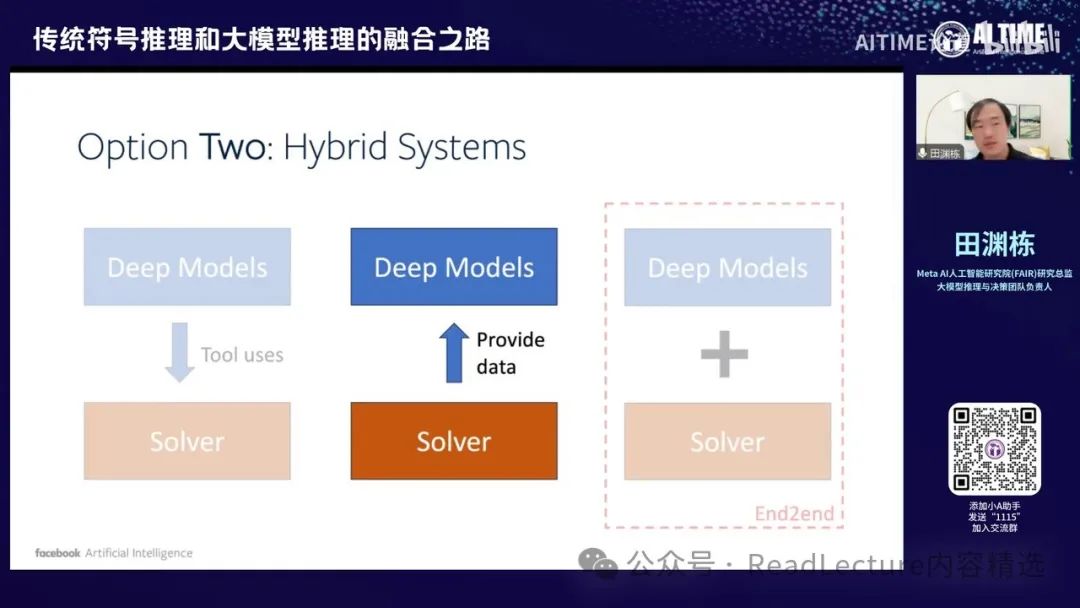
那么第一部分已经讲完了，接下来我们讲一下第二部分的第二个选项。我们如何使用求解器的解来反哺大语言模型，使其变得更强。

大概是这样的，这部分我们主要讲解最近的一系列工作，包括 Searchformer 和 Deformer。这些工作的目的是希望模型能够求解一些较为复杂的规划问题，例如走迷宫或推箱子等。我们现在这个含义非常简单。

在我们输入时，对于迷宫或推理问题，我们输入的prompt是问题的描述。例如，这里是一个3x3的迷宫，每一行表示迷宫的起点和终点，以及哪些地方是不能走的。这些是起点和终点的标志符，后面两个数字是坐标。通常情况下，我们希望在给定问题描述后，能够直接预测最终的规划结果。这大概是最优路径。

但在实际操作中，我们首先通过问题结构的描述调用求解器，这里使用的是A*搜索求解器。求解器会告诉我们求解的细节，包括我们在搜索过程中访问哪些节点和格子，这些节点和格子的位置，以及哪些节点不再访问，最终我们达到目的地。 这个过程中包含了中间的搜索过程，包括遇到阻碍、找到死胡同并返回，整个过程都在其中，最终得到最优解。

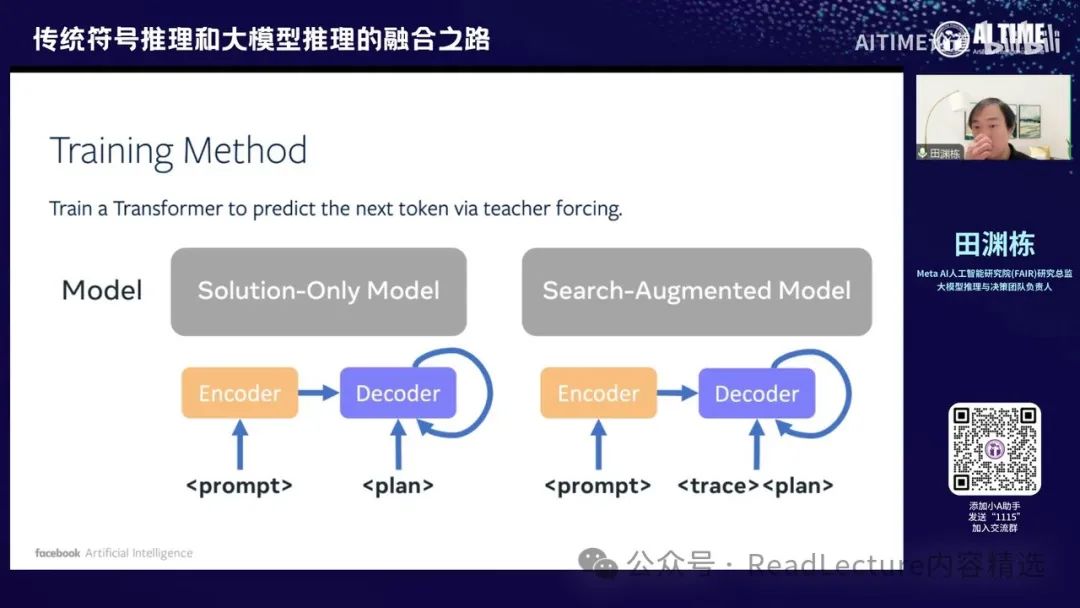
那么这样的话就产生了一个不同的范式。传统上，我们是如何解决问题的呢？我们输入整个问题的描述后，希望模型能够通过自回归的方式直接得到输出的最优解，这是prompt to plan的结构。我们这边的一个改进范式是做search augmented model，即输入问题描述后，我们希望先输出问题的求解过程，其实就是A*求解器的中间步骤，即trace，然后再输出最优的plan。大概是这样的一个过程。然后，后面的trace会非常长，因为一般来说，整个求解器的求解过程是比较长的。

那么你会发现，他的Scaling Law是非常不同的。例如，对于30x30迷宫导航问题，如果使用Solution Only模型，你需要175M的参数和1M的训练样本，才能学到较好的技术。但如果你使用Search Augmented的方法，你会发现只需要15M的参数和100K的训练样本，就能达到类似的效果。因此，通过Search Augmented的范式，你会发现它比直接预测最终答案的方法更高效，无论是数据还是参数。

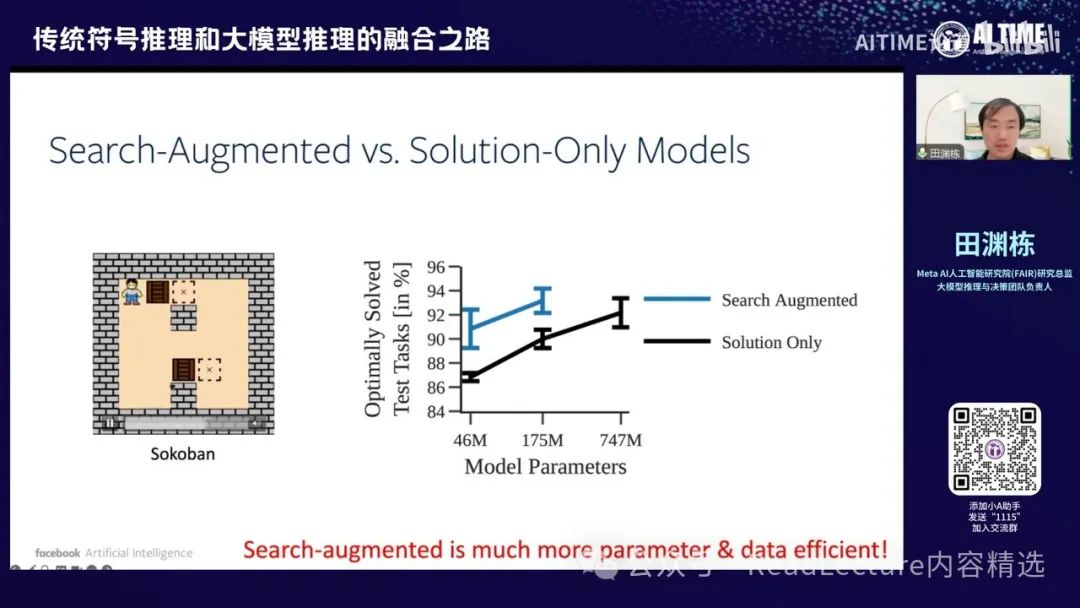
对于某些问题，例如推箱子这类问题，最终结果也是相同的。这是一个简单的问题，即一个人需要推动两个箱子到达目的地，但只能推不能拉。在角度上，如果失败就需要重新开始。通过这种方式，你会发现 search-augmented 比 search-only 更为高效。

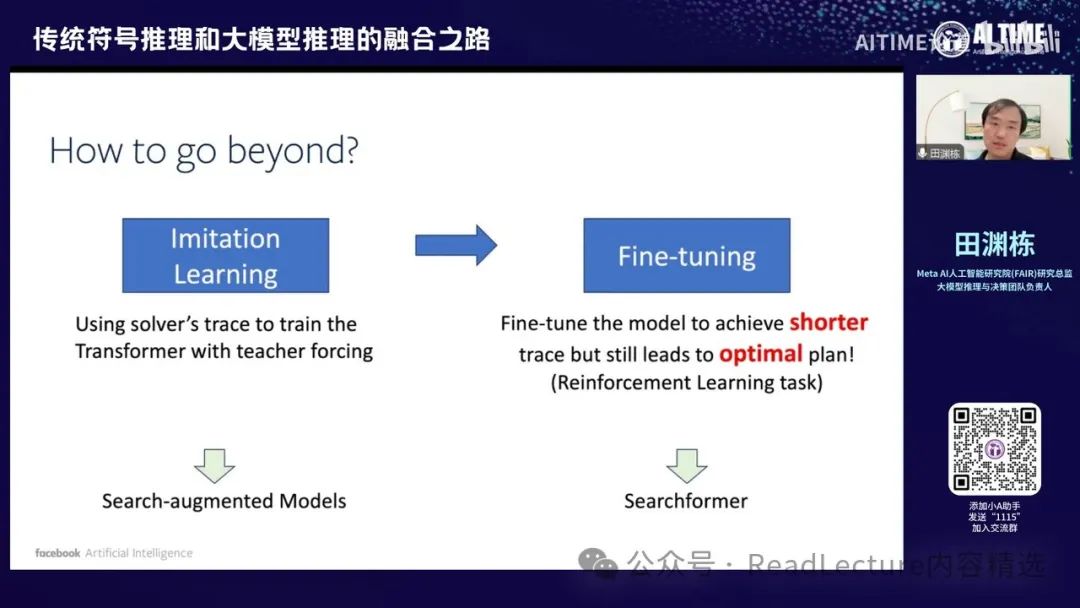
在获得搜索增强模型之后，我们可以进一步改进。由于该模型本身是可微的，因此我们可以通过不断采样来选择那些最终能达到最优解的路径。尽管在达到最优解之前的思考过程或求解器的求解过程中，我们可以找到一个最短的求解路径，但最终仍能得到最优答案。通过这种方式，可以反复提高模型的效率。

每次拿到新模型后，我会让新模型多次采样路径，并找到那些最终得到最优解的路径，然后在这些路径中选择最短的路径，使其仍能得到最优解。这些数据可以用于进一步训练，从而使模型变得越来越强。

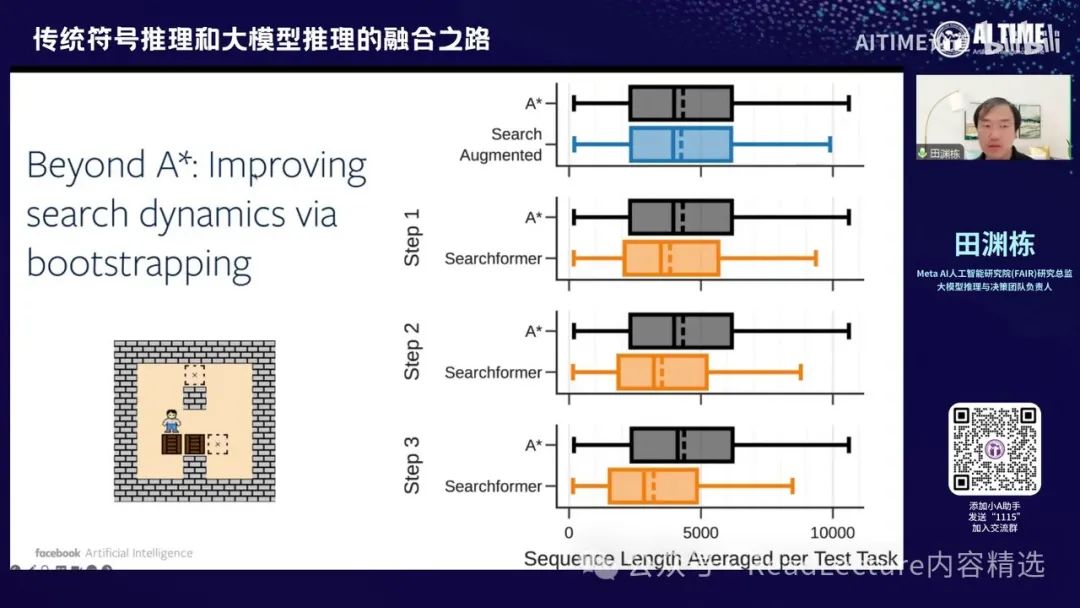
这就是超越A*求解器的思路，你可以看到，从一开始，如果你使用大模型推理，那么这个模型的数据分布，即路径长度，与A*的长度相同。这个路径指的是你整个trace的路径。

在这之后，我们可以通过Searchformer的迭代方式，逐步缩短路径长度，最终答案仍然不错。这种方式可以得到更短的求解路径，但最终的最优解质量不变，甚至更好。

那么这张图片实际上是展示了一些具体的数字，随着每一次迭代，路径的长度逐渐变短，但最优解却在变得越来越好。

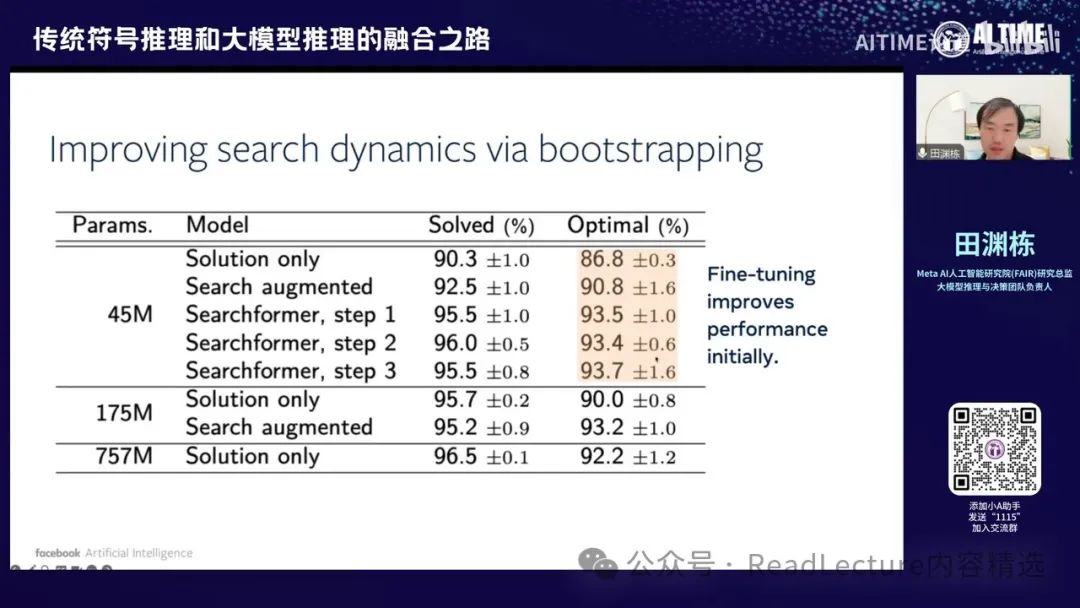
最优解的概率变得越来越大，因此这是一个非常有趣的范式。

在这之上，我们又发表了一篇最新的文章，名为DualFormer，这是Searchformer的第二版。这一版的主要目的是希望求解路径或搜索路径能够稍微缩短一些，因为之前的路径仍然很长。搜索路径中包括各种情况，如碰壁回头、发现问题后返回并找到新路径到达目的地，以及估计未来路径的长度等成本。这些都在搜索路径中。

实际上，你可以通过一些方式缩短搜索路径。例如，可以随机去掉路径中的一些元素，而这些去掉元素的策略可以通过某种方式设计。在这篇文章中，我们找到了一些简单的设计方式，比如去掉整行111，或者去掉最后两个数字，或者去掉其他一些元素。当然，这也包括去掉所有路径的情况。

这个数据生成过程很有趣，你将所有数据放入模型中进行训练，训练出的模型会得到一个很有意思的结果。

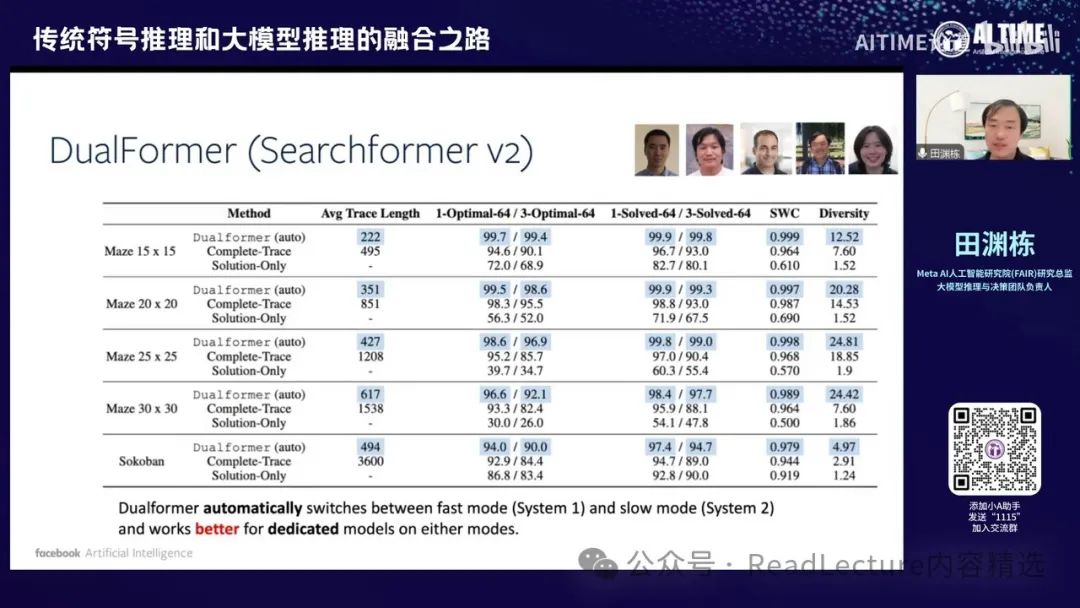
你会发现这个模型虽然输入的数据结构参差不齐，但最终产生了一个有趣的效果：它能自动切换快速推理和慢速推理的过程，自动达到对简单问题快速推理、对复杂问题慢速推理的结果。这很有意思，因为对于人来说，一般有两种不同的推理模式：一种是System 1，即以直觉为准，直接给出答案；另一种是System 2，即非常认真地思考问题，在纸上写很多草稿，经过精确思考后给出答案。通常认为这两种模式需要分别建模，但我们的这篇论文结果表明，通过巧妙生成数据输入的方式，可以训练一个同时具备System 1和System 2能力的模型，并且能够自由切换这两种模式，效果比单独使用System 1或System 2更好。这是一个有趣的现象。

在训练过程中，我们提供了各种可能性，例如一道难题或简单题可能有两种路径：一种是通过搜索路径最终得到解，另一种是直接得到最终解。有了这些不同路径后，神经网络的训练过程变得非常有意思，它通过细化过程可以找到一些偷懒的方式得到最终解。因此，对于简单问题，网络可以很偷懒地找到最优解，不会走错路径；而对于复杂问题，网络必须通过搜索过程才能得到最优解，因此不得不走这条路。这样，网络自然会对简单问题直接预测出最优解，对复杂问题通过搜索路径得到最优解，从而自动实现了对System 1和System 2的切换。

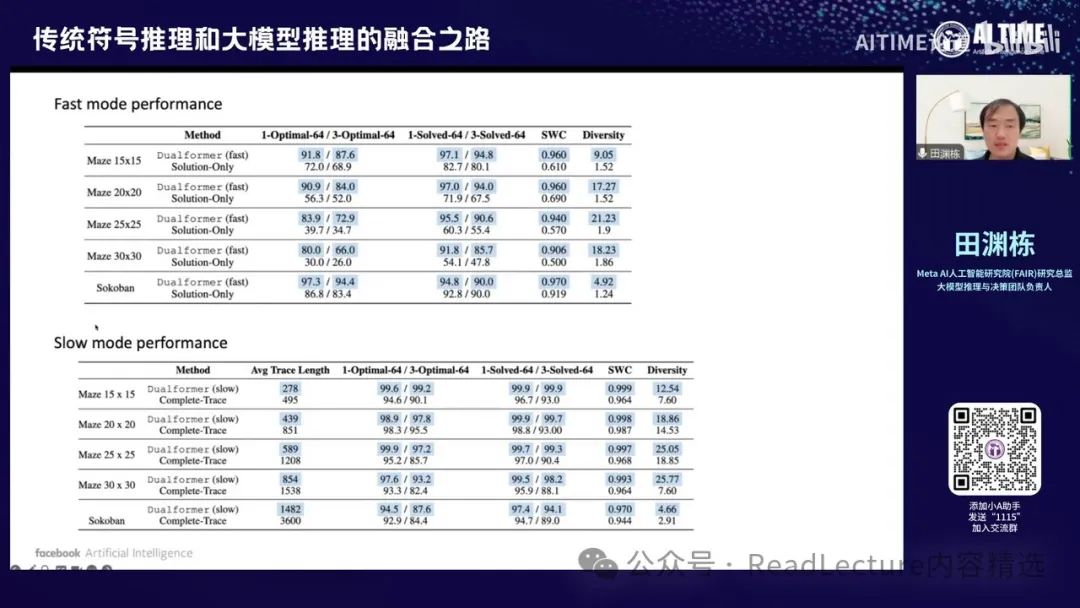
那么我们也可以让Dualformer单独执行系统一或系统二，只需改变第一个token即可。这种方式的效果确实比其他微调方法要好。

那么对于数学问题，我们也尝试过Dualformer的结果。你可能会发现，通过Dualformer，将整个搜索的思维链中的某些单词或句子去掉，然后使用这些数据进行训练。你会发现，训练出来的结果确实能够缩短搜索路径，并且其结果也更为准确。

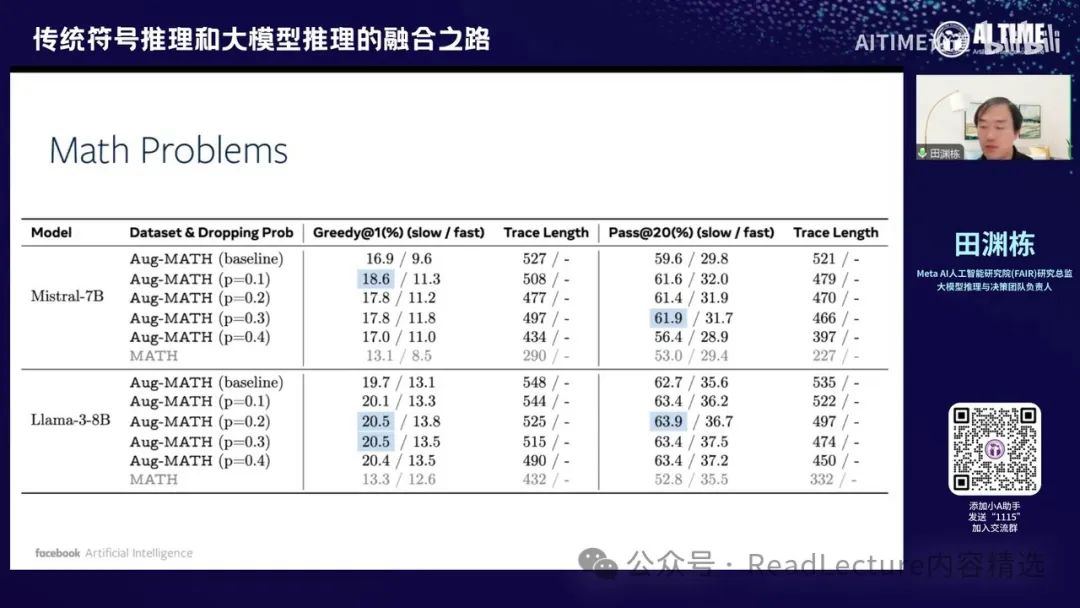
他的性能效果也会变得比原来更好。这是一个非常有趣且令人惊讶的结果。尽管输入的训练数据路径是混乱的，可能中间有跳步，但他最终输出的结果效果其实比原来的模型更好。

那么这是第二部分，Go point option two。然后我们也会讨论一下这个option two的最后一部分，即如何将神经网络与求解器结合起来，直接进行端到端的训练。这是第三部分，这部分呢。

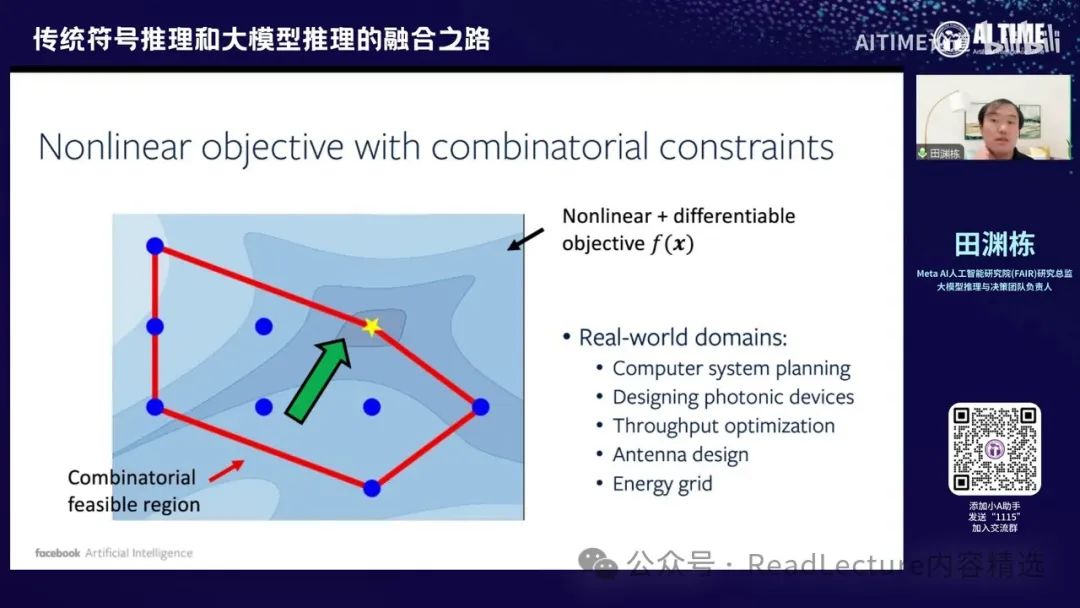
那我们来讲一篇与大模型关系不大但具有实际工业应用意义的工作。 这个工作涉及如何求解非线性问题，该问题包含一个组合优化的可行区域。许多实际问题都具有这种结构，例如神经系统规划、系统设计以及器件设计等。

这些问题本身都非常实际，但由于实际问题中的目标函数多为非线性，传统求解器难以解决这类非线性问题。

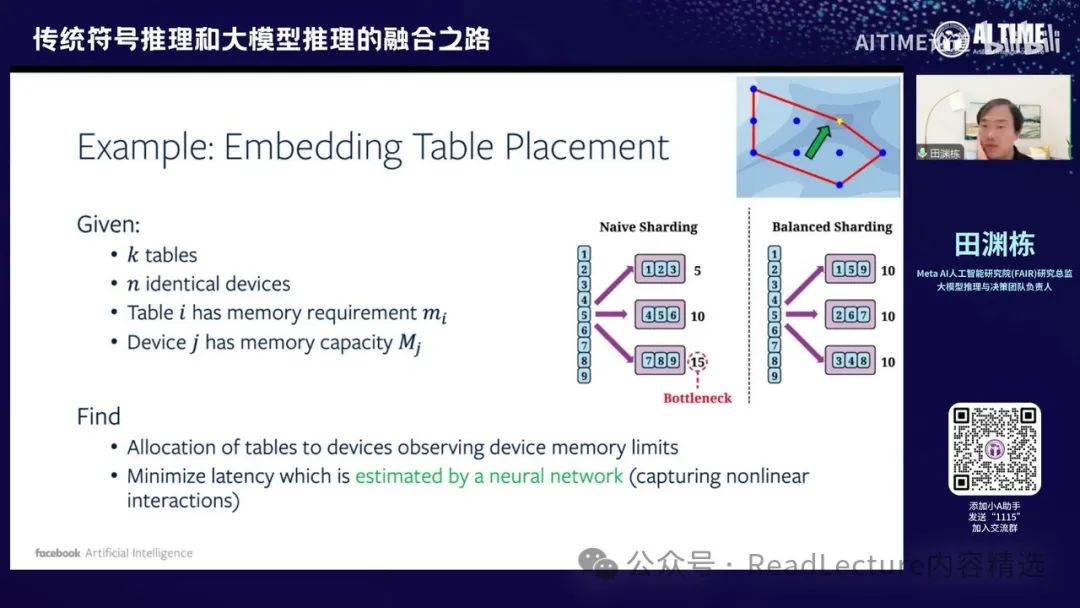
因此，这催生了一篇这样的文章。这是一个例子，假设你有K个表格，这些表格需要被放入N个不同的设备中，这些设备实际上是GPU。这些表格是embedding table，每个表格有自己的内存占用，而每个GPU也有自己的内存容量。因此，存在一些限制，例如一个表格只能放入一个GPU中，不能拆分。

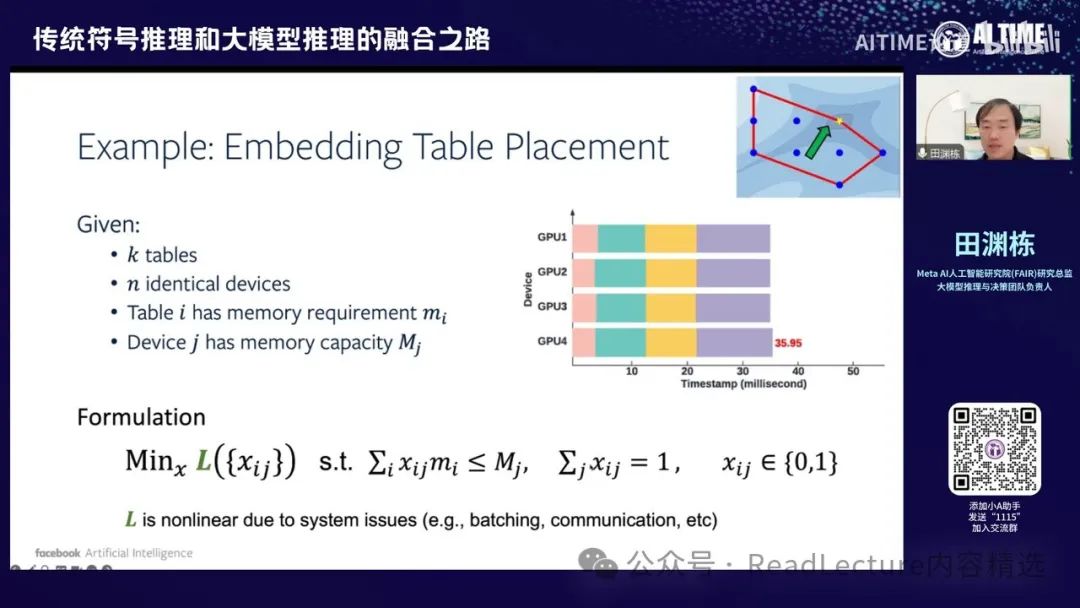
这个限制意味着首先X是一个变量，该变量只能取值0或1。 X的含义是将第I个表格放入第J个GPU中。首先，我们必须确保每个表格至少放入一个GPU中，因此这些变量的和等于1。其次，对于每个GPU，所有放入其中的表格的内存占用量必须小于等于该GPU的总内存容量。

在满足这些条件后，我们需要优化一个函数，该函数可能是整个系统的总延迟时间。由于存在通信、GPU调度等因素，L是非线性的。因此，最小化这个数值实际上需要解决一个非线性的优化问题，但条件本身是线性的，而且是组合的，因为每个X和IJ都是0或1的变量。

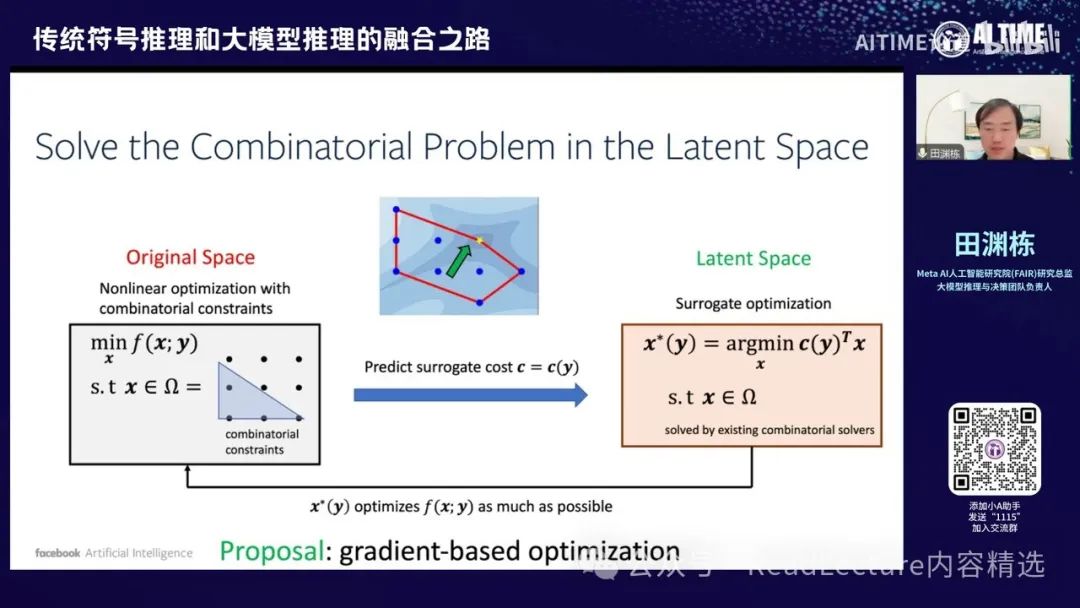
那么这事情怎么做呢？我们当时讨论了一下，对于一开始的空间，即Original Space，你会发现这个问题是一个非线性优化问题，因为F是一个非线性函数，X是要求解的变量，Y是问题的描述。这是一个很难的问题，但我们可以通过某种方式将其变得简单。我们可以找到一个代理的cost，称为Surrogate optimization。有了这个代理之后，我们可以在代理空间中解一个线性问题，这个问题相对容易解。然后，我们将解出的线性问题结果带回去，这个解就是原来非线性问题的最优解。大概是这样的逻辑。通过这种方式，你可能会发现，我们其实可以找到一个比较好的Surrogate optimization，这个优化能够让线性问题的解达到原来非线性问题的最优解。虽然听起来比较绕口，但实际上很容易找到一个解决方案，这个方案就是使用梯度下降，即gradient-based optimization。

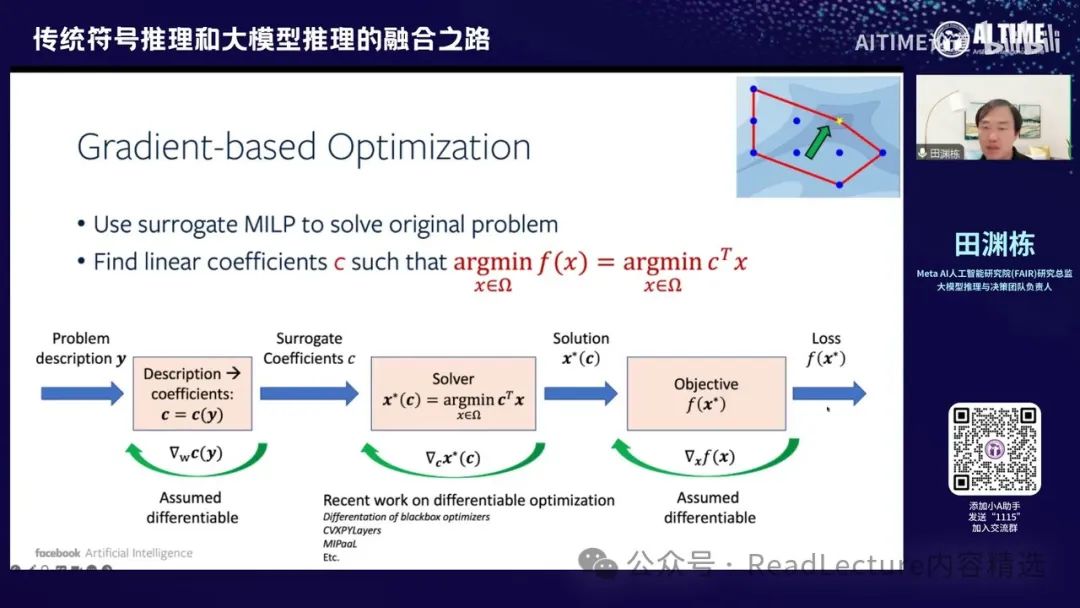
通过优化，首先将整个正向过程写成一个计算图的形式。输入是问题的描述，将其转化为系数，通过某种函数变换后，输入到求解器中。求解器会给出最优解，再将最优解代入目标函数，计算出对应的值。每一步都是可微的，因此可以通过反向传播算法得到梯度，优化最终的映射函数。这个函数可以将问题的描述转化为可用的系数，从而解决一些非线性优化问题。通过这种方式，可以将神经网络与符号表示串联起来，实现反向传递。

那么这部分，我们进行了一些实验，包括刚才提到的Embedding Table Sharding实验。具体细节我就不详细讲解了。

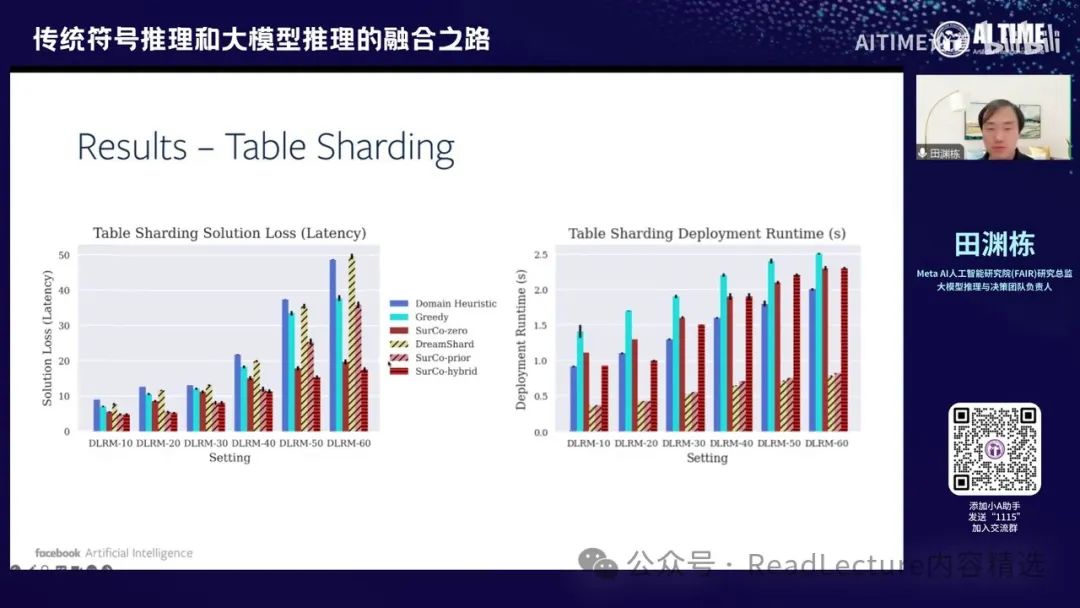
就是说主要的逻辑是我们这种方式，这个算法叫做SurCo。 SurCo有几种变种，比如SurCo-zero，我们通过这种方式在线学习到最优的C，这个C能够解决最终的问题。还有SurCo-prior，我们可以训练一个函数，直接将问题描述转化为C的代价，这样转化非常高效，只需调用求解器就能得到最优解。最后是SurCo-hybrid，结合了这两者的优点。

你会发现，相比其他基准方法，首先，SurCo得到了最终的损失函数值较小；其次，延迟也较短，因为SurCo-prior直接预测一次C就能得到最优解，不需要反复调用求解器，所以非常快。而SurCo-hybrid兼顾了两者的优点，得到的solution loss较少，这是一个比较好的平衡。因此，我们比那些基准方法要强一些。

当然，我们可以用这种方式来解决其他问题，例如另一个设计问题——逆向光子设计（Inverse Photonic Design）。在一个非常小的80×80纳米的区间块内，你需要放置各种点。每个点的黑白状态是一个设计目标，目的是希望设计完成后，能够将上方射来的光通过某种方式扭曲到左边和右边去。

通过这种方式，这四个图会更加清晰。例如，最下面的四个图，其中一个图表示光从上方下来，通过设计内部的花纹，使光折射到左边。另一个图表示光从上方下来，通过这些花纹变成两束光。这些结构需要设计，因为对于很小的这条线，你无法在其中放置镜子，所以必须利用光的电磁波性质来实现分光器或旋转器。

这个问题是一个优化问题，且目标函数非常复杂。你需要使用麦克斯韦方程模拟光的行进路线，得到一个反馈函数，然后进行傅里叶变换，得到频域上的反馈，再用这些反馈计算出一个复杂的函数，这就是最终的原函数。此外，它本身也有许多约束条件，例如每个点上只有0和1两个解，这些0和1的结构必须连成一片，因为最终生成这个东西时，需要用一个小刷子去刷，如果有点是1，周围那些点也必须是一，这有最小半径的概念，这也是一个经济条件。这些条件加在一起后，问题变得比较复杂。

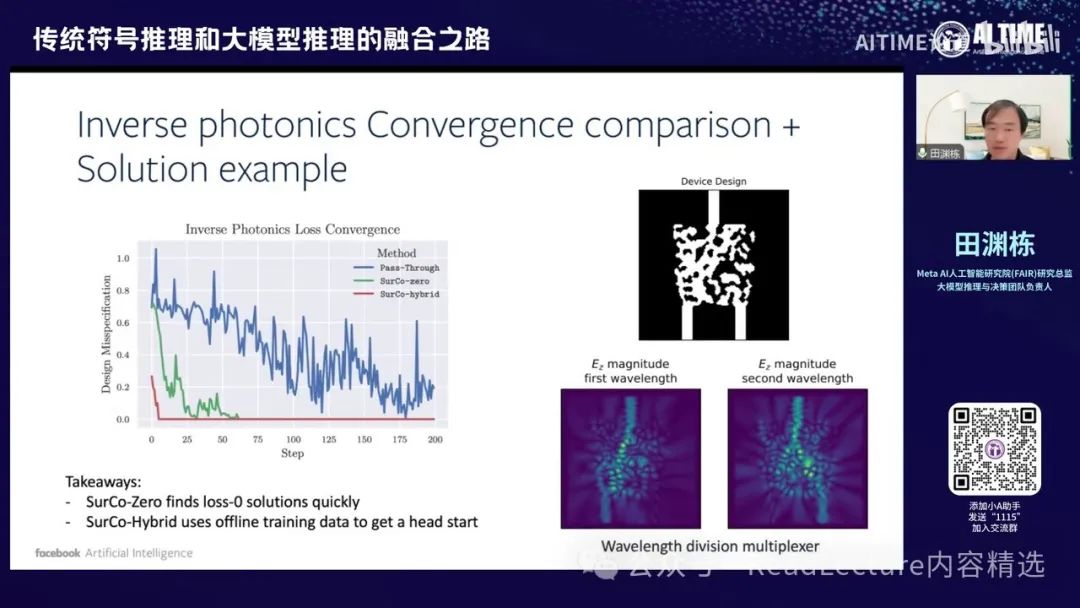
但是，我们正好可以采用这种方法。通过将神经网络与最终的求解器相结合，你会发现其最终的收敛速度实际上比传统极限算法更快。这是一个非常有前景的应用。

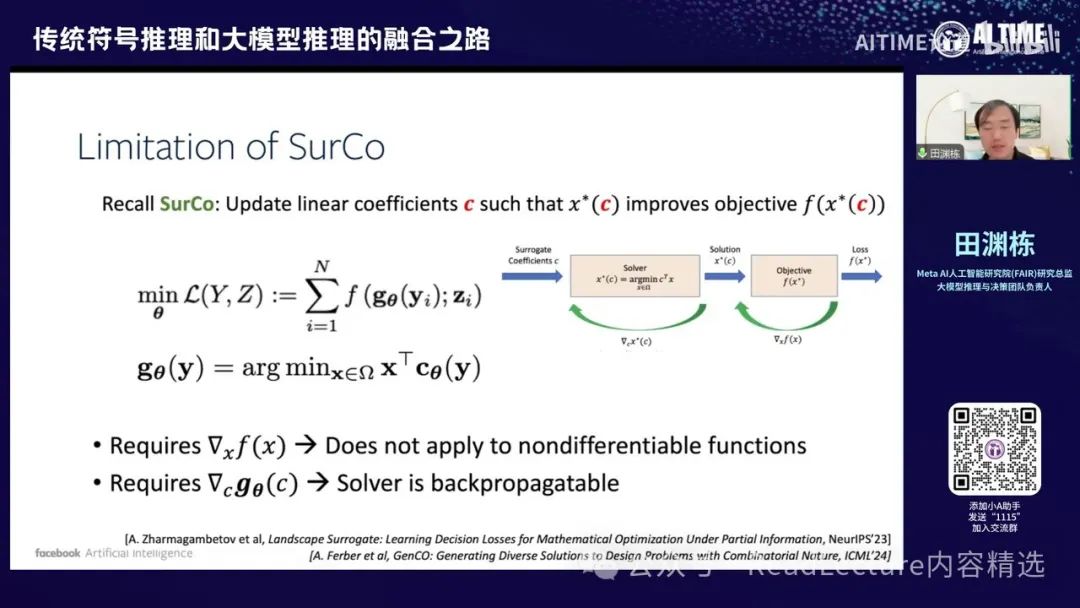
因此，最后我们还有这个幻灯片，它指出这种方法存在许多问题。接下来，我们还有两篇文章，将进一步解决这些问题。

最后，我们可以稍微讲一下这三部分的第三部分。虽然我们大多数人都会认为神经网络的结构和符号系统的结构是并行的，且完全无关的。我们经常提到有神经学派和符号学派，这两派在过去的人工智能领域中观点对立。然而，这两派观点各有优势，有些问题可能更适合用符号来解决，而有些问题则更适合用神经网络来解决。传统上，这两派被认为是水火不容的。但实际上，通过对神经网络收敛解的研究，你会发现其中其实存在着符号结构。这个符号结构可以通过理论构建出来，并且你会发现这个符号结构与初始下降解的结构是能对上的。因此，也许最终你会发现，梯度下降解出来的解可能正好通向一个符号的解释。这是一个非常有趣的现象。当然，实际上有很多符号系统，也有很多问题，什么样的问题是一个比较有意思的。

一个我们可以讨论的问题，肯定是涉及到当前的神经网络。

当前的大模型确实具有一些有趣的性质，因此我们当然希望找到一个具体的任务，这个任务能够充分展示出大模型或当前语言模型的一些短板或有趣的现象。

关于大模型，一方面，大家认为通过大量参数的堆积，我们可以看到许多新能力的涌现，这种现象被称为emergent behavior。因此，大家为什么要研究大模型呢？就是因为大模型能够产生许多以前不具备的奇妙现象，我们相信大模型有一天能够带领我们进入超人工智能的境界。这是一种观点。

另一种观点认为，Scaling Law可能并不有效，因为有大量证据表明大模型在处理推理问题时，并非进行真正的推理，而只是在检索以往的知识。这一观点的依据是，大模型在一些简单任务上会犯非常愚蠢的错误。例如，有一篇从Apple内部来源的文章，名为"js m a k symbolic"，其主要逻辑是，如果你在大模型中输入一句与问题无关的话，数学大模型的效果会突然变差。

当然，这个观点并不新鲜。因为之前DANNY周在Google团队中也有类似的文章，讲述过同样的故事。这个问题早已为人所知，但一直未得到解决。

那么，当这两派在争论时，你可能会思考，大模型是否具备深入理解和学习推理问题的能力。目前，这个问题尚无定论。这涉及到如何对推理问题进行有效的人工表示，这种表示是否能够泛化到其他情况下。

对于这篇文章，我们可以先解决一个较为简单的问题，称为Modular Addition。这是一个非常简单的推理问题，即两个数A和B相加得到C，我们的目标是预测C。给定A和B，我们希望计算出C。当然，这里的加法是取模加法，意味着A、B和C都在0到D-1的范围内，D是模数。

这个问题很简单，因为你可以将所有可能性都记录下来，形成一个大表格，包含所有A和B的取值，表格中的数字是C的取值。一旦这个大表格建立起来，问题就变成了一个检索问题。然而，有趣的是，如果你将这些数据作为神经网络的输入和输出，并希望神经网络学习这种映射时，你可能会发现神经网络并没有使用表格。

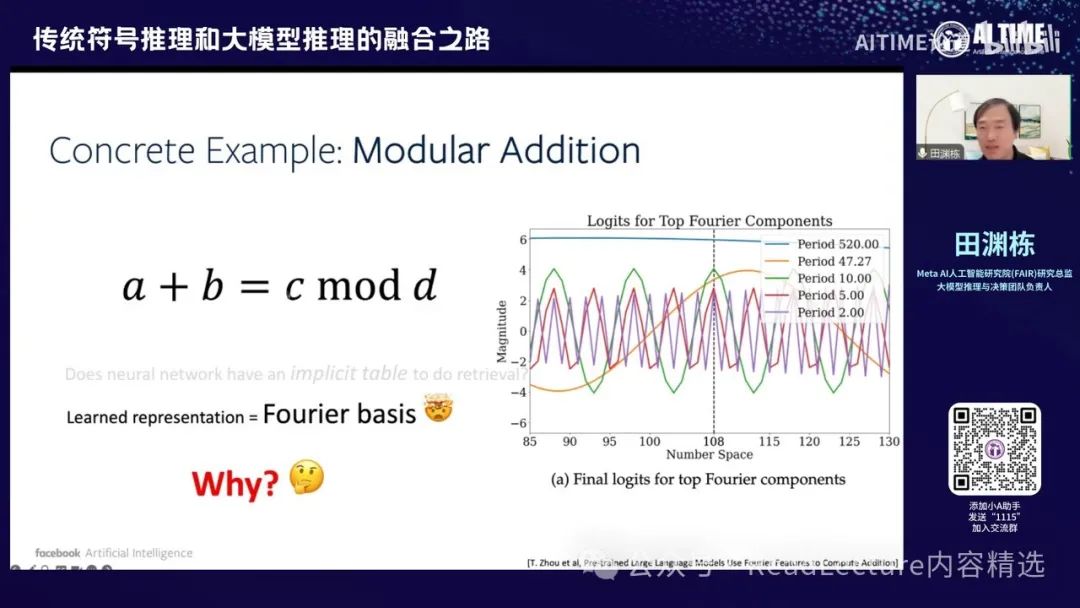
然后记录下来，神经网络使用的是傅里叶变换，即它学到了一个傅里叶变换的表示。这个表示用于进行加法运算，这是一个非常有趣的现象。 这种现象已经被许多人观察到，包括最近的一篇文章指出，预训练的大模型中实际上使用了傅里叶变换的特征来计算加法。你可以看到许多正弦和余弦函数。

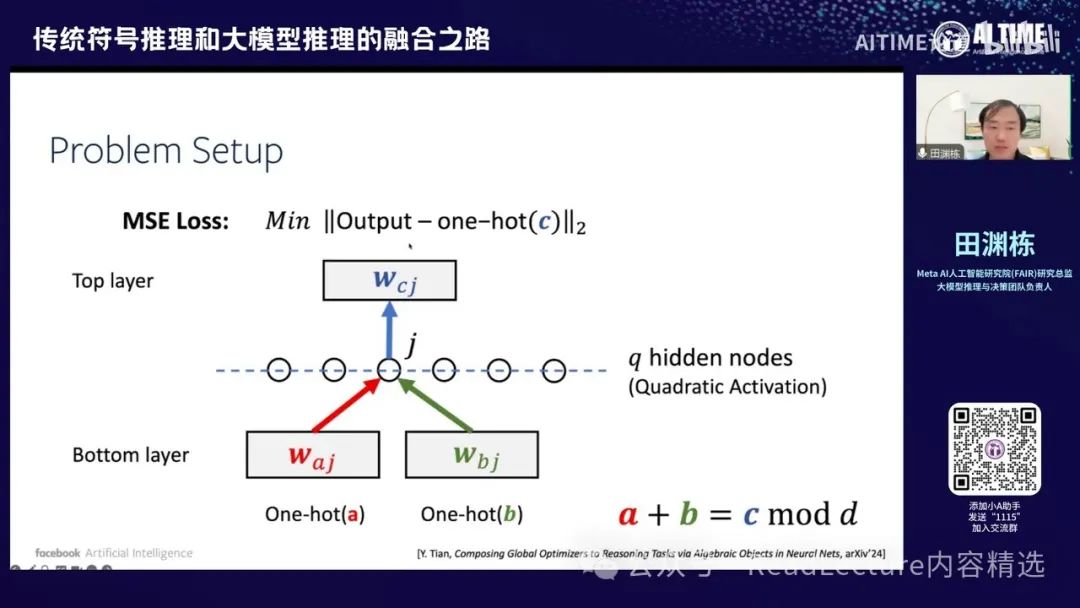
在这个图中，如何解释或分析这个现象其实是一个很有意思的问题。我们使用了一个比较简单的设定，例如使用两层的神经网络，输入是两个W，输出是一个位置，然后得到一个loss。

输入时，先将A和B转换为one-hot表示，然后将它们连接起来，经过下面一层，计算出一个值，再经过一个非线性的神经元，即Quadratic Activation，然后经过上一层，最终输出一个结果。这个输出要与one-hot表示的C进行比较，C是你最终的答案。两个数字越接近越好，所以最终的loss使用平方loss，这是一个非常简单的设定。因为它最终的结果是傅里叶变换，所以涉及到sin和cos函数。

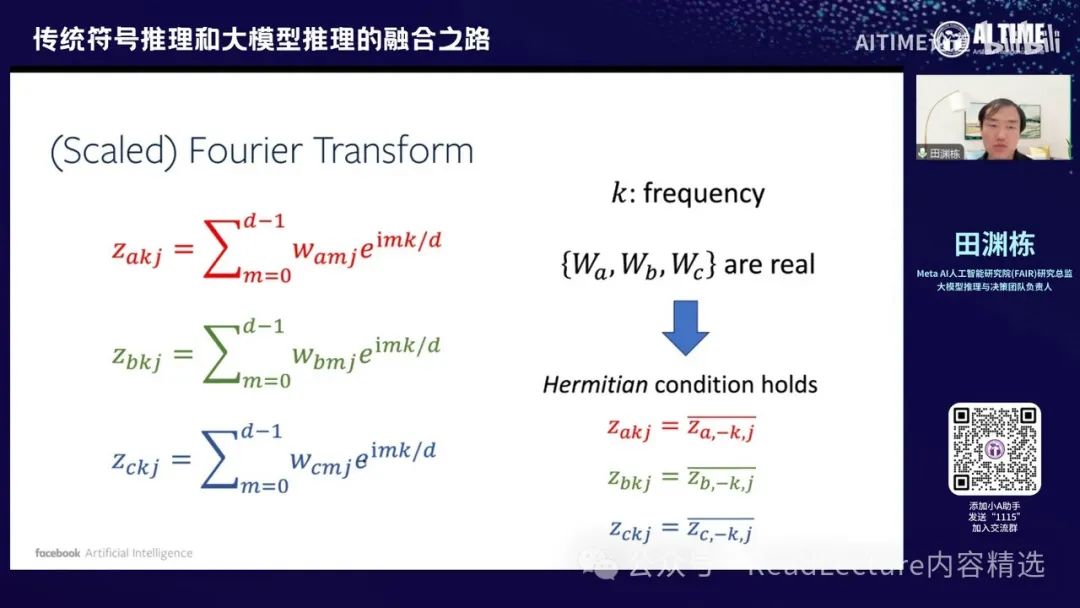
因此，我们这边首先对其进行了傅里叶变换。

做完傅里叶变换之后，你会发现其解释非常清晰，并且具有对称性的结构。这是一个重要的发现。首先，横轴表示你有多少个隐藏节点，这是底层节点的索引。纵轴表示每个隐层节点上的傅里叶变换。由于D为7，所以频率从0到6，共有七个不同的频率。你会发现，对于每个频率，相应的隐层节点数目正好是六个或四个。例如，六个隐藏节点在平面上亮起，这边也有六个隐层节点亮起。

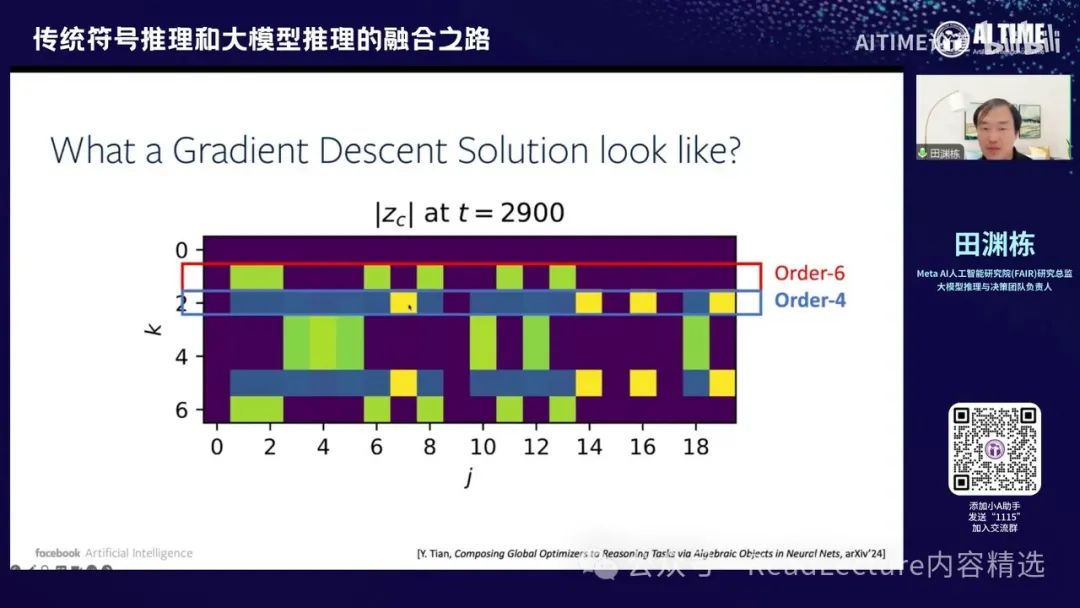
所以这是六个order six的解，还有一些解是order four，即1234。你会发现有四个节点是两强，而其他的一些节点则相当于是一个较小的BIOS，这是order four的解。这个结构很有意思，即在经过训练后，这个结构最终凝结成了一个代数的，或者说在数量上具有一定特征的结构。

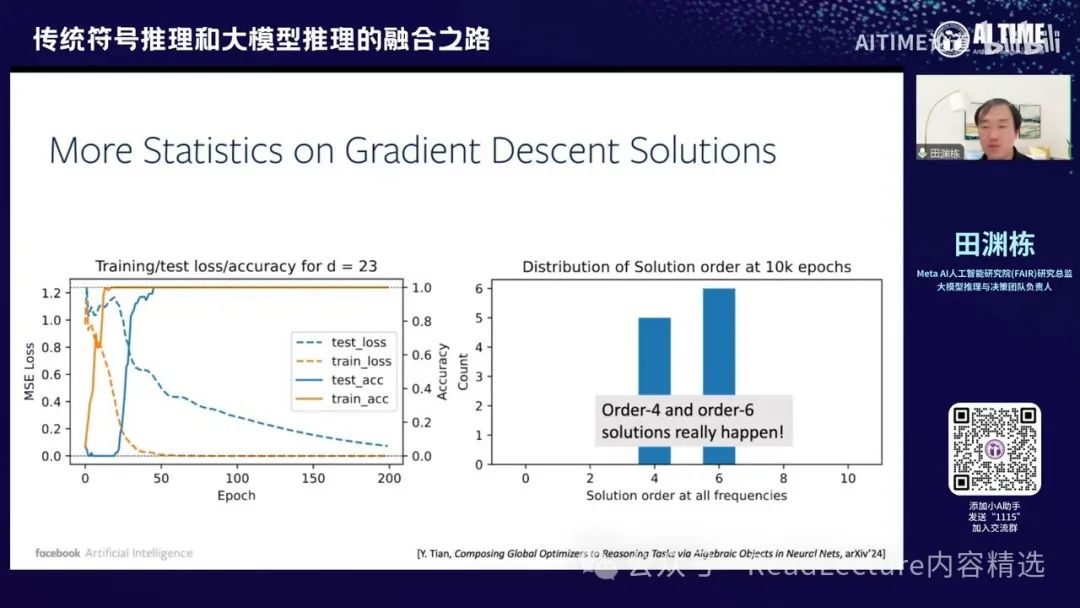
或者说是组合上的一个结构，这很有趣。 如果你将这个问题变得更加复杂，例如将D变为23，D越大，结构越复杂。当你处理123时，你会发现需要检测每个频率上神经元的数量，即在特定频率上是否有分量。你会发现有许多神经元对应于order-4的solution，还有一些频率对应于order-6的solution。如果画成直方图，你会看到这样的分布。

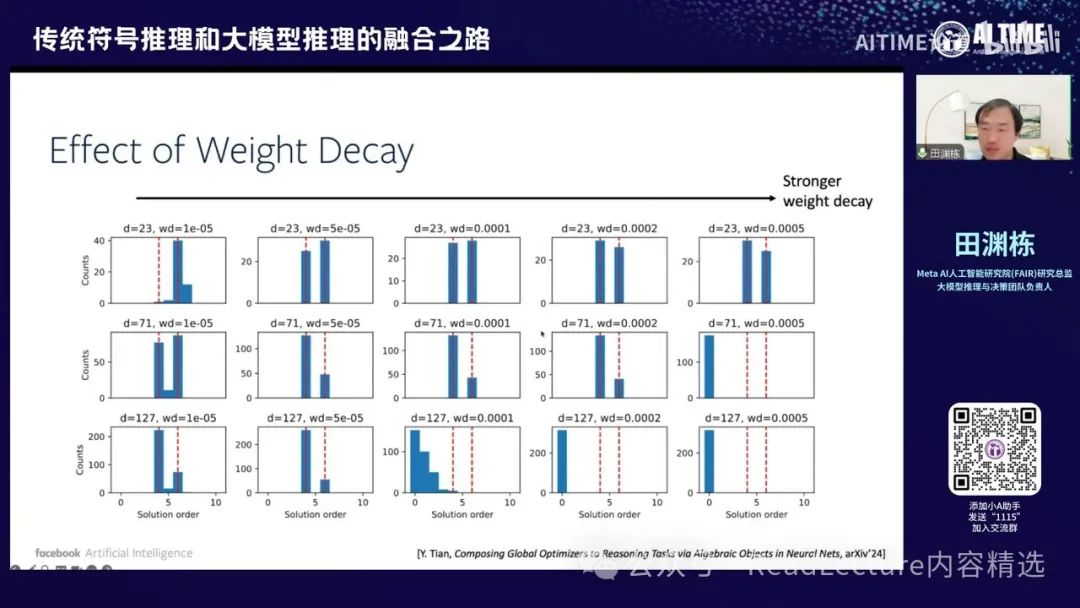
如果你将这个问题或实验做得更复杂或更全面，例如，我这里有三个不同的D，分别是237、11和127，纵轴表示同样的D，但横轴表示不同的VDEK来进行优化。你会发现，在大多数情况下，最终会出现两个峰值，一个是六，一个是四。没有其他峰值出现，这两个峰值在很多情况下都会出现。这是一个非常有趣的现象。

这篇文章其实讲述了一个可能的原理，这个原理涉及到神经网络中的一些代数结构。 这个结构比较有趣。首先，我们可以将MSE loss（均方误差损失函数）写成一个复杂的形式。这个形式包括第一项，以及许多平方和项。第一项是一个线性项，大概是这样子。这里每个项包括R和NRK1K2K以及RPK1K2K，这些项其实是一些东西的加法。J是所有神经元的和，直接是神经元的角标。他将隐藏的角标隐藏的东西全部加起来，然后得到这样的一个项。

所以这个式子其实与你有多少个神经网络、有多少神经元是没有关系的。 如果神经元有100个、1000个或1万个，这个式子永远是长这样子，没有什么区别。所以这个很有意思，因为有这个式子之后，你可以对不同宽度的神经网络做一个统一的代数结构。代数结构有一些很有意思的性质。

那么，给您这个L2的平方和，你就可以在这上面写一些充分条件。这些条件就是说，如果这些条件满足的话，我们就能找到它的最优解。条件很简单，就是第一项为1，后面所有的平方和都是零，这时就是最优解了。

但是大家可能会觉得这个条件没有用，因为条件非常非常非线性，你不知道这里面解到一些什么。但是很有意思的是，这个问题本身存在一个非常有趣的代数结构。这个结构是什么样子呢？ 就是如果你把所有的神经网络，他的输入和输出固定的神经网络，只有隐藏层不一样的神经网络放在一起，变成一个整个集合，叫Z1。这个集合Z1包括了所有的二层神经网络，输入是2D，输出是D，这样一个神经网络，但它中间隐藏层的大小是不一样的，有些大有些小。那么这个Z1其实内部有一个结构，这个结构叫semi-ring的结构，即半环结构。有了这个半环结构之后，你其实可以通过这个结构来构造这个问题的一个最优解，就是这样的一种想法。

那么如何构造呢？非常简单，就是说，比如我们之前写下的那个损失函数，这个损失函数里面有几项，包括这些R项，对吧？然后，如果我们找到一个部分解，称为pass solution，这个部分解只将一个R变为零，而其他R则不为零，这就是一个部分解，因为这部分解相对来说比较容易找到。

由于整个神经网络具有这种半群半环的结构，我们可以将两部分拼起来，变成一个解，这个解能够同时满足两个R都等于零的条件。也就是说，如果你有Z1，它满足了一个红颜色的R等于零的解，而Z2是那个绿色R的解，那么将这两个数字乘起来，但这个乘法不是普通的乘法，而是群上和环上的乘法。乘完之后，你会发现最终的Z1能够同时满足红颜色的R和绿颜色的R。通过这种方式。

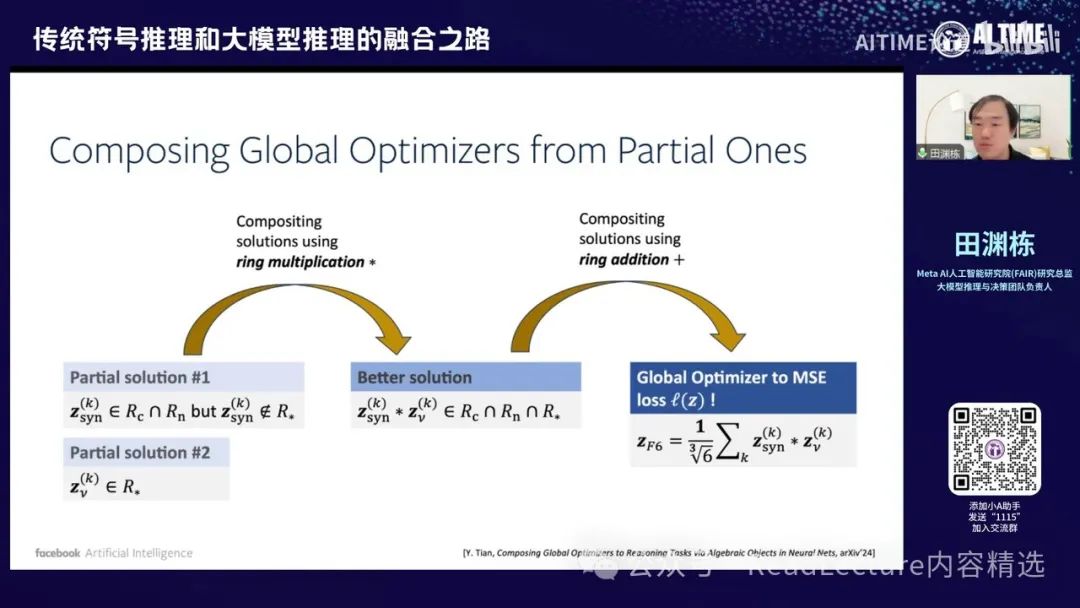
你可以从小的解逐步构造出大的解，最终构造出整个目标函数的全局最优解。通过这种方式，你可以构造出这样的结论。因此，这个图的意思是，你先构造出一些较小的、满足某些子条件的解，将这些解相乘后，能够满足更多条件，再将这些解相加，最终得到一个解。这个解能够满足整个损失函数的全局最优解。

通过这种方式，你可以构造出不同order的解决方案。Order指的是每个频率上需要激活的神经元数量，这些神经元对应的频率必须有相应的分量。通过这些频率分量的组合，你可以构造出一个order-6的解。这个order-6的解实际上是通过2和3的组合来实现的，即你有一个order-2的解，满足一部分条件，再有一个order-3的解，应用条件将它们相乘，得到一个order-6的解，满足所有条件。然后将每个频率的分量相加，最终得到一个较好的解。这些解实际上都是损失函数的全局最优解。

这可以证明，当然，构图这个解本身并不稀奇，因为有很多方法可以构造出这个解。但有趣的是，这个解构造出来后，其结构与你真正通过梯度下降得到的解的结构是一样的。这是一个很有意思的现象。

如果你将最终通过梯度下降得到的解拿出来，首先检查这些解是否满足order 4和6，结果是满足的。其次，你按照半环乘法的方式对这些order 4和6的解进行分解，你会发现它们真正能够分解成2×3和2×2的格式，而这个格式本身正是你之前构造的解的结果。这个现象很有意思。

另外，当你真的将这些分解成两部分后，让每一部分与你之前构造的order 2和2×3的解进行比对，你会发现分解出来的部分其实就是我们之前构造的那些小部分解的一个特例。因此，我们的理论实际上与最终的实践是相连的，你会发现理论构造出来的解就是实验上得到的解。

这是一个非常有趣的现象。 最终，我们来看一下具体解的分布，其中包含了一些有趣的结构。这些结构本身，我们目前只是作为观察结果，但尚未进行解释，留待下一篇文章再做详细探讨。

这篇文章中一个有趣的地方是，我们现在能够找到一个较好的解决方案，但之前通常是通过梯度下降来实现的。也许存在另一条路径，即通过代数结构的方式来得到归类SN的解。 这意味着，也许有一天，我们可以抛弃梯度下降，直接通过代数方法得到最优解。这可能是一种可能性，尽管目前还无法实现，但这是一种很有趣的可能性，能够将符号系统和神经网络系统最终结合起来，形成一个统一的整体。